Data strucutres and Dojo
(2ys ago)
Hello There🐼
Let's talk Data Structures.
In this blog we will talk about how we can use these data structures smartly to solve problems rather than what these data structures actually are.
Following picture shows typical classification of different data structure.
A bunch of things arranged in an ordered manner, which can be accessed by their index value is what a typical definati on of an Array.
Typical operations you might encounter while using Arrays
I will be using python lists to demostrate various operations on arrays.
Insertion
There are many ways and places where you can insert elements in an array such as
- At the begining
- At the end
- At some index
Let's say you have an array of numbers from 1-10.
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]Insertion operations.
1 list.insert(position, element)
Python gives you a built in method on list to insert at any given position.
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
arr.insert(0, 0)
print(arr) #[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
arr.insert(len(arr), 11)
print(arr) #[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]2 list.append(element)
Insert element at the end of the list.
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
arr.append(11)
print(arr) #[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]3 list.extend(anotherList)
Appends another list to the current list.
arr1 = [1, 2, 3, 4, 5]
arr2 = [6, 7, 8, 9, 10]
arr1.extend(arr2)
print(arr1) #[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]Deletion
1 list.remove(x)
It removes the first occurance of the provided element x.
⚠️⚠️ It will throw an error if the value is not found in the array ⚠️⚠️.
arr = [1, 2, 3, 4, 5]
arr.remove(2)
print(arr) #[1, 3, 4, 5]
arr.remove(0) # Throws an error ⚠️
2 list.pop([i])
We can use pop() in two ways
- Remove the last element
- Remove the element at a given position
arr = [1, 2, 3, 4, 5]
arr.pop() # Removes last element
print(arr) # [1, 2, 3, 4]
arr.pop(0) # Removes element at position `0`
print(arr) # [2, 3, 4]3 list.clear()
Cleans out the whole array.
arr = [1, 2, 3, 4, 5]
arr.clear() # Removes all elements
print(arr) # []Sorting
Sorting is basically arranging the elements in the array in increasing or decreasing order. Sorting is a topic for another day.
In Python there two ways you can sort the list
1 list.sort()
- It sorts the array inplace.
- Uses
TimSort algorithmto sort the array inplace.
arr = [5, 4, 3, 2, 1]
arr.sort()
print(arr) # [1, 2, 3, 4, 5]2 merge sort algorithm
There are many sorting algorithms but the famous one is merge sort with time complexity of O(n.log(n)).
characteristics of merge sort:
- inplace sorting algorithm.
O(n.log(n))time complexity.- Reccursive algorithm.
Here is the simple implementation of merge sort. Watch this youtube-video to learn more.
def split(arr) -> None:
if len(arr) < 2:
return
left = arr[:len(arr)//2]
right = arr[len(arr)//2:]
split(left)
split(right)
merge_sort(arr, left, right)
def merge_sort(arr, left, right) -> None:
# Get the length of Left and Right sub arrays
L = len(left)
R = len(right)
i = j = k = 0
while (i < L and j < R):
if left[i] <= right[j]:
arr[k] = left[i]
i += 1
else:
arr[k] = right[j]
j += 1
k += 1
# Edge Case
while (i < L):
arr[k] = left[i]
i += 1
k += 1
while (j < R):
arr[k] = right[j]
j += 1
k += 1
arr = [5, 4, 3, 2, 1, 0]
split(arr)
print(arr) # [0, 1, 2, 3, 4, 5]Searching
Searching an element in the array.
1 list.index(x)
- This method returns the index of the element
xin the array.
arr = [5, 4, 3, 2, 1]
index = arr.index(3)
print(index) # 22 Binary Search algorithm
The array should be sorted to do perform binary Search.
def binary_search(arr, val) -> int:
left, right = 0, len(arr)-1
while left <= right:
mid = left + (right - left) // 2
if arr[mid] == val:
return mid
elif arr[mid] > val:
right = mid-1
else:
left = mid+1
return -1
arr = [1, 2, 3, 4, 5]
index = binary_search(arr, 4)
print(index) # 3Maximum Subarray
It is a problem from leetCode you can find it at 53. Maximum Subarray.
Various approaches to solve this problem
- Brute-force: Try all possible subarray and return the one which has maximum sum.
- Kadane's algorithm.
To solve this problem we are going to use kadane's algorithm for better optimizaiton.
Kadane's algorithm
Consider the following array in which we have to find the maximum sum subarray.
- Kdane's algorithm goes from starting index and keeps adding the next item in the list.
- After addition of the next item if the sum goes to negative it is sure that that sub array will make ur total sum even lesser. Then in that case we have to make a fresh start.
- We drop the subarray which will give us lesser sum or say negative sum value.
- We do a fresh start off and then do the same thing till the end of the array.
def maxSubArray(nums: list):
currMax: int = 0
maxMax: int = min(nums) # It is done so that we do not
# miss boundary case like if the nums
# array is only one element.
# nums = [-1]
for num in nums:
currMax += num
# The sum is getting negative do a fresh start
if currMax < 0:
currMax = 0
# We might have found a solution update the maxMax value
if currMax > maxMax:
maxMax = currMax
return maxMax
nums = [1, -2, 3, 4, -1]
max_subarray = maxSubArray(nums=nums)
print(max_subarray) # 7
# [1, -2, 3, 4, -1]
# ^ ^
# | |
# | |
# +Two-sum
It is one of the most famous interview and leetcode question.
Ways to solve it:
- You can Brute force your way out.
- Use a
hashmap/dictionaryto save the values of the array corresponding to their indices. - We will loop through the array.
- For every element we calculate the residue amount i.e;
currentNumber - target. - In simple terms how much do we need to add to the current element to make up to the target.
- If we find that the residue is available in the array through
hashmap/dictionarylookup then we return the positions. - Else we store the current number in the loop as the key with it's index as the value.
def twoSum(nums: list, target: int):
# Creating an empty dictionary
allVals = dict()
for i, num in enumerate(nums):
residue = target-num
if residue in allVals:
return [allVals.get(residue), i]
allVals[num] = i
return []
nums = [2, 7, 11, 15]
target = 9
ans = twoSum(nums, target)
print(ans) # [0, 1]An array restricted to only two possible operations possible is a stack. You can push or pop from the stack from only one end.
Operations on stack
Push and pop
- stack and array are similar to each other.
- stack has limited insertion and deletion operations compared to an array.
- In stack you can only insert or remove elements from one end of the array.
- You can imagine stack as a
khada hua array. - It follows FILO i.e;
First in Last out.
# Usually we restrict insertion and removal to be done from the front of the array.
# Here i have restricted it to back of the array, and it is completely okay!!
# As i am retaining the most important characteristic of the stack i.e; FILO.
stack = [1, 2, 3, 4, 5]
popped = stack.pop()
print(popped) #5
print(stack) #[1, 2, 3, 4]
stack.append(5)
print(popped) #5
print(stack) #[1, 2, 3, 4, 5]Typical problem you can solve using Stack
- Palindrome matching
- Parentheses matching
and some more....
Palindrome matching
You can use stack to store a number or string to reverse it and check if that number or string is palindrome or not.
XWe will write a function that takes in a string as an input and checks wether it is palindrome or not, which returns either True or False.
def palindrome_or_not(word) -> bool:
# Convering the word into stack
word = [x.lower() for x in word]
# temp stack to check the palindrome charecter.
temp = word.copy()
for w in word:
if w != temp.pop():
return False
return True
palindrome_or_not('madam') # True
palindrome_or_not('vercel') # FalseA queue is simply horizontally lying list, in which we restrict insertion and deletion operation to only one end
Operations on queue
1 Creation of deque
Python has inbuilt deque method through which we can define our queues.
from collections import deque
d = deque('abcd') # make a new deque with four items
print(d) # deque(['a', 'b', 'c', 'd'])2 Insertion in deque
deque.append(): Insert at the Right end of the queue.deque.appendleft(): Insert at the Left end of the queue.
from collections import deque
d = deque('bcd')
print(d) # deque(['b', 'c', 'd'])
d.append('e') # deque(['b', 'c', 'd', 'e'])
d.appendleft('a') # deque(['a', 'b', 'c', 'd', 'e'])3 Deletion in deque
deque.pop(): Remove element from Right end of the queue.deque.popleft(): Remove element from Left end of the queue.
from collections import deque
d = deque('abc')
print(d) # deque(['a', 'b', 'c'])
d.pop() # deque(['a', 'b'])
d.popleft() # deque(['b'])4 Rotation in deque
deque.rotate(n): Ifnis positivecircular right shiftelsecircular left shift.
from collections import deque
d = deque('abc')
print(d) # deque(['a', 'b', 'c'])
d.rotate(1) # deque(['c', 'a', 'b'])
d.rotate(-1) # deque(['a', 'b', 'c'])The idea of Linked List is to have a memory efficient data structure.
About Linked List
- We store data in the nodes.
- Each node has
dataandreferencepart. - There are multiple variations of Linked List. such as
Single Linked List
- Only one link exists between 2 nodes.
- You can only traverse in one direction.
- There is no connection betweenn present and previous node.
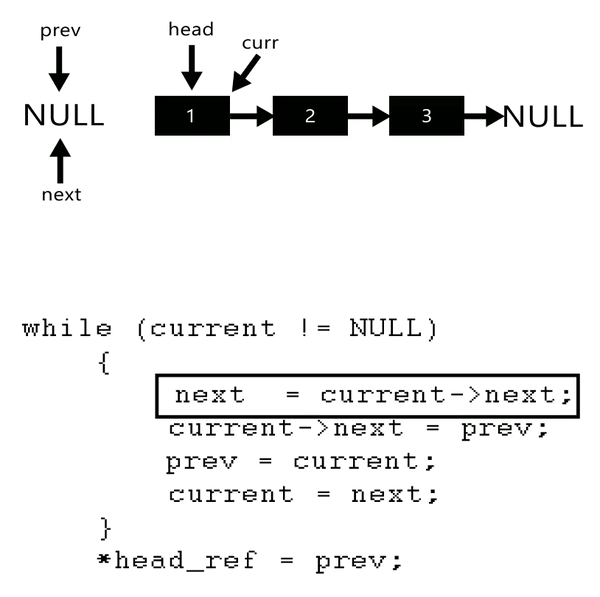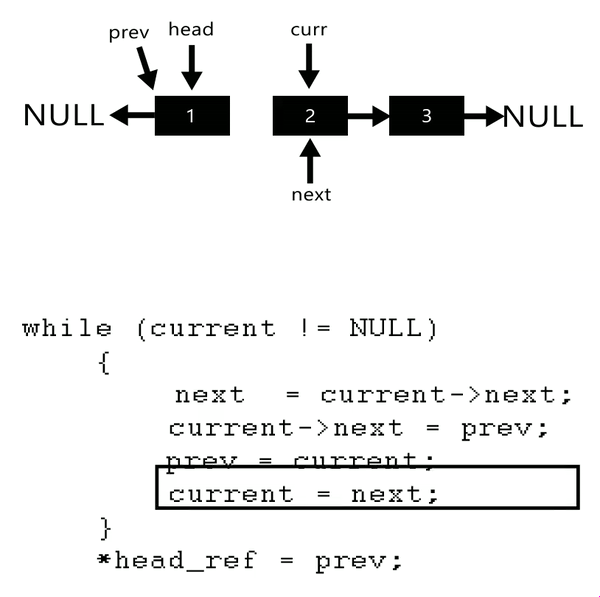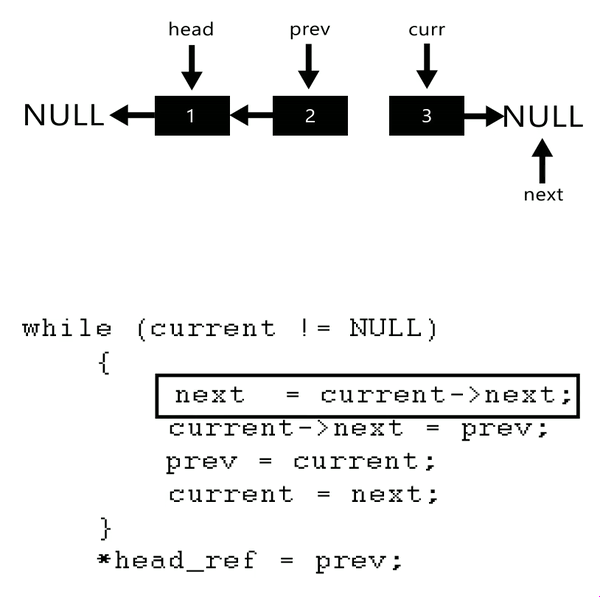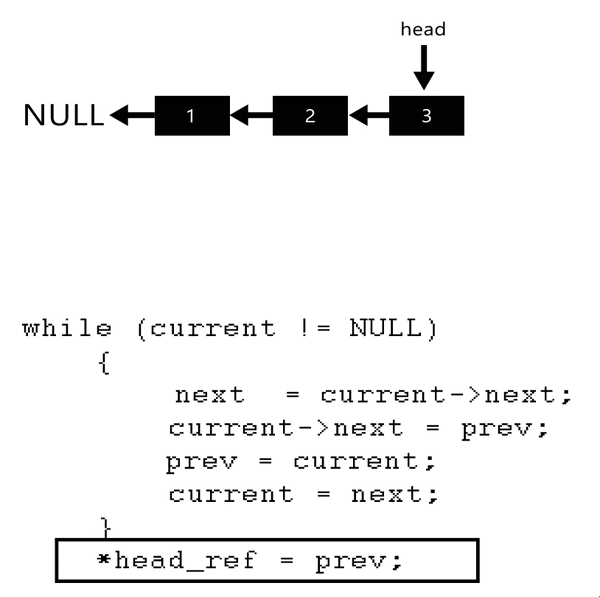
Reversing a single linked List
- You will need three pointers to do this.
Prev,currandnext
Intialize the list as shown in the figure.
2 The following Code snippet performs the operation shown in the
.gif.
Doubly Linked List
- Two links exists between 2 nodes.
PrevandNext. - You can traverse in both direction.
- Pointer memory overhead
Circular linked list
- Two links exists between 2 nodes.
PrevandNext. - You can traverse in only one direction.
- The last node's
nextpointer points toheadnode.
Circular Doubly linked list
- Two links exists between 2 nodes.
PrevandNext. - You can traverse in both direction.
- The last node's
nextpointer points toheadnode.
It is a non-linear hierarchial data structure consisting of nodes and edges used to represent data such that it is easy to navigate and search.
About Trees
-
We store data in the nodes and connect to other nodes through edges.
-
There is no restrictions on insertion and deletion of the elements in the tree.
-
There are many trees data structure. Some important ones are listed here.
-
Traversel in Trees:
Binary Tree
- Each parent node has at-most two child nodes.
- classification based on the number of child node.
| Measure | Condition | Formula |
|---|---|---|
| Minimum nodes | Height -n | n + 1 |
| Maximum nodes | Height -n | 2n+1-1 |
| Maximum Height | Nodes -n | n + 1 |
| Minimum Height | Nodes -n | loge2n |
Complete Binary Tree
All the levels of the tree aare completely filled except for maybe last level.
Perfect Binary Tree
- All the leaf nodes are at same deapth.
- Each node has exactly two or zero child nodes.
Binary Search Tree
- Each parent node has at-most two child nodes.
- Very useful for searching operations.
- While insertion:
- Element less than the root node goes to
left. - Element greater than the root node goes to
right.
- Element less than the root node goes to
- While deletion:
- If it is a leaf node, then simply delete it.
- If it has one child, then simply replace the node with it's child.
- If it has two children:
- Look at the right subtree of the node to be deleted, and replace it with the node with
leastvalue from right subTree. - OR
- Look at the left subtree of the node to be deleted, and replace it with the node with
maximumvalue from right subTree.
- Look at the right subtree of the node to be deleted, and replace it with the node with
Traversal
Preorder Traversal
- First element is the root.
Inorder Traversal
- You get the elements in ascending order.
postorder Traversal
- Last element is the root.
Graph is just a bunch of nodes or data points connected with each other through edges.
Exploring the graph
- There are two ways to explore the graph
Sample graph
Deapth First Search
- Uses stack.
- Go as deep as possible and trackback is the concept.
Aplications
- Check if the graph has cycle.
- Find path from source to destination in graph.
Simple implementation
def dfs(graph, src) -> None:
visited = list()
stack = [src]
while stack:
vertex = stack.pop()
if vertex not in visited:
visited.append(vertex)
print(f'Explored {vertex}')
stack.extend(
neighbour for neighbour in graph[vertex] if neighbour not in visited)
# Sample graph
graph = {
'A': ['B', 'C'],
'B': ['D', 'E', 'A'],
'C': ['F', 'A'],
'D': ['B'],
'E': ['F', 'B'],
'F': ['C', 'E']
}
dfs(graph, 'A')Breadth First Search
- Uses queue.
- Go level by level.
Aplications
- Find shortest path in a directed graph.
- Finding solution to a problem which invloves finding least number of possible moves.
Simple implementation
from collections import deque
def bfs(graph, src) -> None:
visited = list()
queue = deque([src])
while queue:
vertex = queue.popleft()
if vertex not in visited:
visited.append(vertex)
print(f'Explored {vertex}')
queue.extend(
neighbour for neighbour in graph[vertex] if neighbour not in visited)
# Sample graph
graph = {
'A': ['B', 'C'],
'B': ['D', 'E', 'A'],
'C': ['F', 'A'],
'D': ['B'],
'E': ['F', 'B'],
'F': ['C', 'E']
}
bfs(graph, 'A')Good Day 🐼